What is a Radian?

Last week I spent some time reviewing what the CCSS say about trigonometric functions. As I was reading I came across a standard that made me pause.

CCSS.MATH.CONTENT.HSF.TFA.1: Understand radian measure of an angle as the length of the arc on the unit circle subtended by the angle.

So I'll be honest, radians are still a bit mysterious to me. So I did some digging around in Sameer Shah's Virtual Filing Cabinet, and I came across Kate Nowak's blog post encouraging teachers to ask their students "what is one radian?" I then decided that I would write a post doing by best job to explain what is one radian.

Roger Cotes is credited for the concept of radian measure in 1714, however the term radian did not come about until 1873. The radian is considered the standard unit of angle measure. Radian measure depends on arc measure on the unit circle.

The measure, in radians, of an angle subtended by a circle arc is described as the length of the arc on the unit circle, divided by the radius. Wait...what is an "angle subtended by a circle arc"?

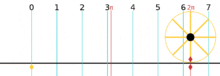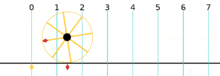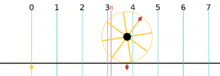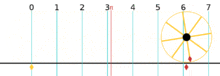
So this means that one radian is the angle subtended by an arc that is equal to the radius of the circle. So in other words an angle with measure 1 radian has an arc length of 1 on the unit circle.

An angle with radian measure pi (which we know is 180 degrees) has an arc length of 3.14159...Which means there are pi radians in 180 degrees.

So again, one radian is the angle subtended by an arc that is equal to the radius of of the unit circle. 

Another observation that comes from the use of radians is that the circumference of a circle is 2pi times the radius of the circle. The circumference can be thought of as the length of the arc of the entire circle, or as my high school math teacher taught me, the distance it takes to walk all the way around a circle.  So this would mean that the circumference of the unit circle is equal to the radian measure of a 360 degree angle ,  Well we know that the radian measure of a 360 degree angle is 2pi, so that means that the circumference of the unit circle is also 2pi. When we say that the circumference of a circle is 2pi*r, we are really just counting the number of "radii" that make up the exterior of the circle. 

In most mathematics angles are generally measured in radians because radians are more "natural", there are no degrees or meters attached to this measure so this allows radians to be unitless. It is very important that students understand the concept of radian measure, not just because the Common Core State Standards state its important but because using radians makes math easier! Trigonometric functions are defined by ratios in the same way radians are defined by ratios, so it only makes sense to use radians while working with trigonometric functions. However, it is important that students have a deep understanding of radians before they begin to work with them, it is important for students to know exactly what a radian is. When students have conceptual understanding of ideas like this it will only help their understanding of other mathematical concepts.